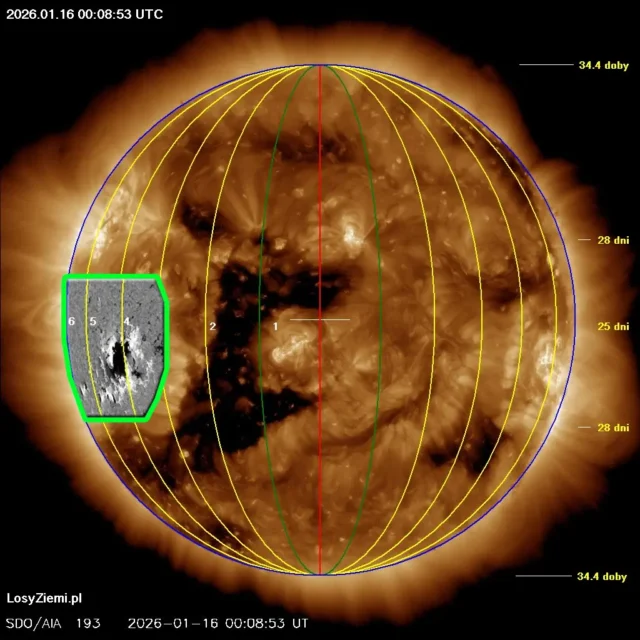
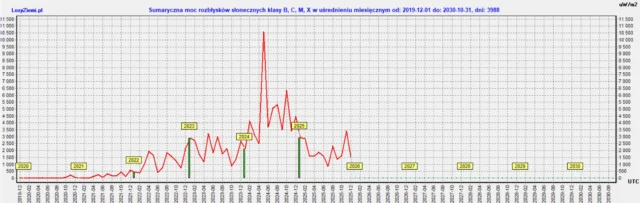
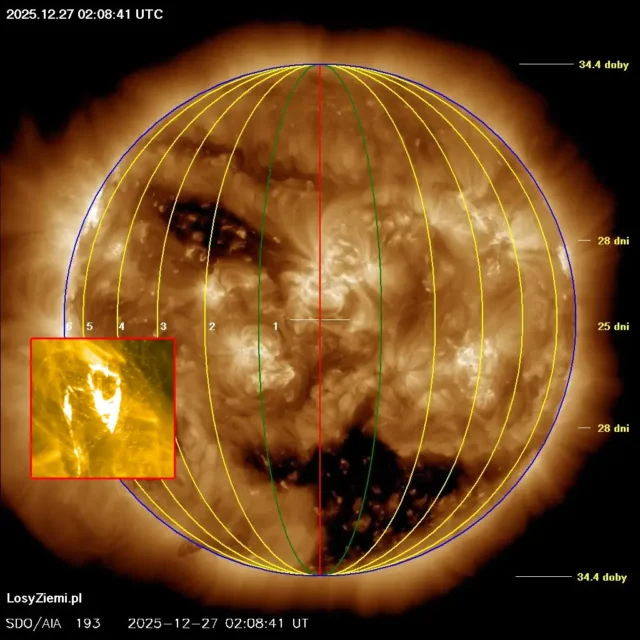
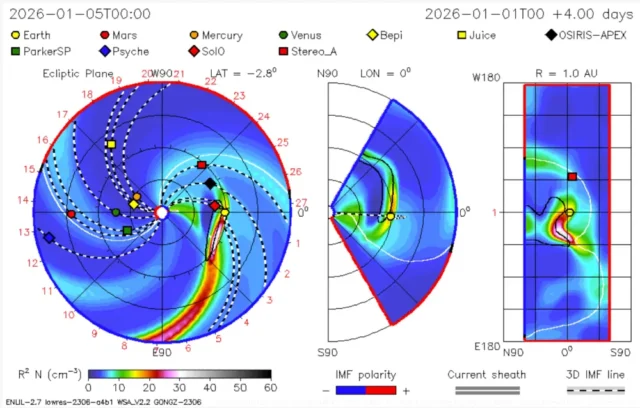
◄ Treść dostępna po zalogowaniu. ►
◄ Zaloguj się. ►
Trwa zbiórka darowizn na utrzymanie serwisu, więcej informacji po prawej stronie.
Zasady wsparcia finansowego serwisu, jak również możliwości otrzymania konta opisane są TU.
Trwa zbiórka darowizn na utrzymanie serwisu, więcej informacji po prawej stronie.
Zasady wsparcia finansowego serwisu, jak również możliwości otrzymania konta opisane są TU.
W styczniu zebraliśmy tylko:
Szybka wpłata anonim.
z czego cała reszta czytelników spoza grupy VIP: 0.0%